Camera Focus in Computer Vision: A Guide

Camera focus in Computer Vision refers to the adjustment of optical lens of camera to ensure that the captured image is sharp and clear for objects at a specific distance from the camera. When an object is in focus, its details and edges appear well-defined in the image. If an object is out of focus, it becomes blurry and its features are less distinguishable.

Measuring camera focus with computer vision involves analyzing the sharpness of the captured image to determine if the object is in focus. The sharpness is quantified by assessing the amount of high-frequency detail in the image, which is reduced when the image is blurry (out of focus).

Ensuring proper camera focus is crucial for accurate data collection and inferencing in a computer vision system. The sharpness of images directly impacts the effectiveness of models trained for tasks like object detection, defect identification, or quality control. Poor focus can lead to blurry images, making it difficult for models to extract meaningful features, resulting in errors, missed detections, and lower accuracy.

Imagine a manufacturing plant deploying a computer vision-based defect detection system for coffee beans for quality control. The system is tasked with identifying issues such as discoloration, irregular shapes, or damaged beans on a conveyor belt. If one of the cameras in the system becomes misaligned or out of focus:

• Defects might not be detected because the model cannot process blurry images effectively.
• Several defective coffee beans could pass undetected down the production line, increasing costs for rework or refunds.

The image below demonstrates a coffee bean defect detection model detecting defects in coffee beans. In the left section (a), where the image is properly focused, the model accurately identifies defects. However, in the right section (b), where the image is slightly blurred and out of focus, the model's performance deteriorates, failing to identify defects effectively.

To address this issue, an automated camera focus monitoring system is needed which work as follows:

• Each camera continuously measures focus and focus value is monitored in real-time against a predefined threshold.
• If the focus value falls below the threshold, the system triggers an alert for the operator to intervene.
• The engineer adjusts the camera focus manually while observing the real-time visualization of focus values on a dashboard.
• As the camera reaches optimal focus, the system confirms and resumes operation.

We will now see how to build a camera focus monitoring system that can automatically measure focus quality by capturing images, evaluate their sharpness using a focus measurement algorithm, and trigger an alert if the camera goes out of focus.

Here is an example showing camera focus calculation in use:

Camera Focus Methods

There are many methods and techniques used for camera focus measurement (as discussed in this paper), we will focus on the following three methods.

• Variance of Laplacian
• Brenner Function
• Tenengrad Function

Variance of Laplacian

The Variance of Laplacian is a method used to measure the sharpness or blurriness of an image. It quantifies the amount of edges present in an image by computing the variance (i.e., the spread) of the Laplacian filtered image. A higher variance indicates a sharper image with more edges, while a lower variance suggests a blurrier image with fewer edges. Let’s understand how it works.

The Laplacian operator is a second-order derivative that calculates the rate of intensity change in an image. For a 2D image f(x,y) the Laplacian is given by:

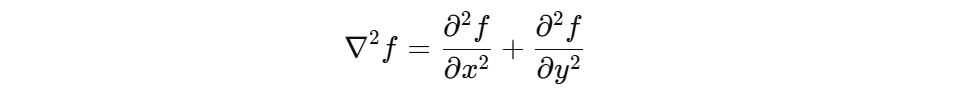
In the context of digital images, this is implemented using a discrete convolution kernel, such as:

Applying this kernel to an image emphasizes regions with rapid intensity changes (edges). The result of applying the Laplacian operator to an image is a new image L(x,y), called the "Laplacian image," where each pixel value represents the intensity of edges at that location. Variance is a statistical measure of how spread out the values in a dataset are. For the Laplacian image L(x,y), the variance σ2  is computed as:

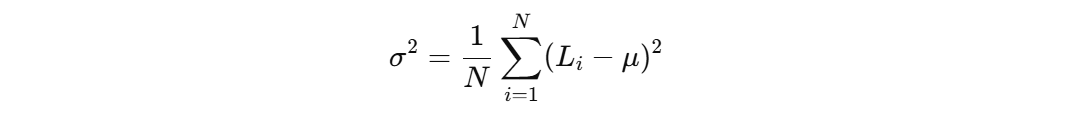
Where:

• N: Total number of pixels in the image.
• L_i : The intensity value of the i-th pixel in the Laplacian image.
• μ: The mean intensity value of the Laplacian image.

This formula calculates the average squared difference between the Laplacian values and their mean, which measures how much the edge intensities vary. Following are the steps in code to calculate the Variance of Laplacian for an image to measure its sharpness or focus.

Step #1: Convert Image to Grayscale

The Laplacian operator is applied to a single-channel image, therefore the input color image needs to be converted to grayscale.

gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

Step #2: Apply the Laplacian Operator

The Laplacian operator detects edges by finding regions of rapid intensity change in the grayscale image. cv2.Laplacian computes the Laplacian of the grayscale image.

laplacian = cv2.Laplacian(gray, cv2.CV_64F)

The resultant laplacian image contains edge intensity values. Positive and negative values indicate the direction of intensity changes.

Step #3: Calculate Variance

The variance of the Laplacian measures the spread of edge intensities, indicating image sharpness. .var() is a NumPy function that computes the variance of all pixel values in the laplacian image.

variance = laplacian.var()

High variance indicates sharp image and low variance indicates blurry image. Following is the code for camera focus using Variance of the Laplacian.

import cv2
import numpy as np

def calculate_laplacian_focus(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    laplacian = cv2.Laplacian(gray, cv2.CV_64F)
    variance = laplacian.var()
    cv2.putText(
            laplacian,
            f'Focus value: {variance:.2f}', 
            (10, 30), 
            cv2.FONT_HERSHEY_SIMPLEX, 
            1, 
            (255,),  # White color in grayscale
            2
        )
    return variance, laplacian

def monitor_focus():
    cap = cv2.VideoCapture(1)
    if not cap.isOpened():
        print("Error: Camera not accessible.")
        return
    
    focus_threshold = 600

    while True:
        ret, frame = cap.read()
        if not ret:
            break

        focus_score, laplacian = calculate_laplacian_focus(frame)
        status = "In Focus" if focus_score > focus_threshold else "Out of Focus"
        color = (0, 255, 0) if status == "In Focus" else (0, 0, 255)

        cv2.putText(frame, f"Focus value: {focus_score:.2f}", (10, 30),
                    cv2.FONT_HERSHEY_SIMPLEX, 1, (255, 0, 0), 2)
        cv2.putText(frame, status, (10, 70), cv2.FONT_HERSHEY_SIMPLEX, 1, color, 2)

        # Normalize laplacian for display
        laplacian_display = cv2.normalize(laplacian, None, 0, 255, cv2.NORM_MINMAX)
        laplacian_display = np.uint8(laplacian_display)

        cv2.imshow("Laplacian Focus Monitoring", frame)
        cv2.imshow("Laplacian Focus Measure Image", laplacian_display)

        if cv2.waitKey(1) & 0xFF == ord('q'):
            break

    cap.release()
    cv2.destroyAllWindows()

if __name__ == "__main__":
    monitor_focus()

The code will generate output similar to following, showing the camera focus measurement changing as we adjust the camera focus:

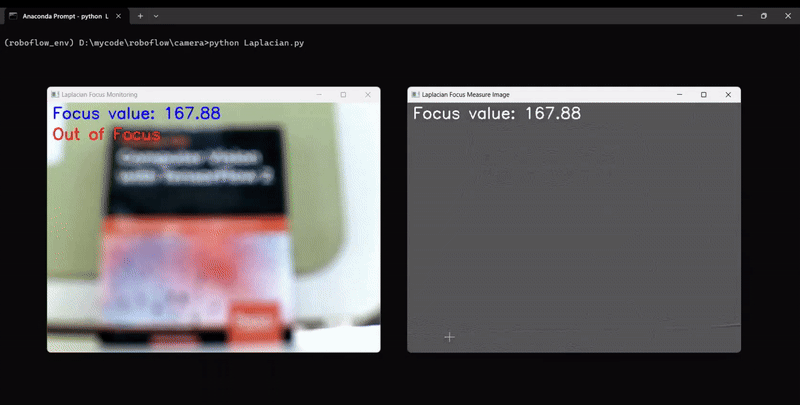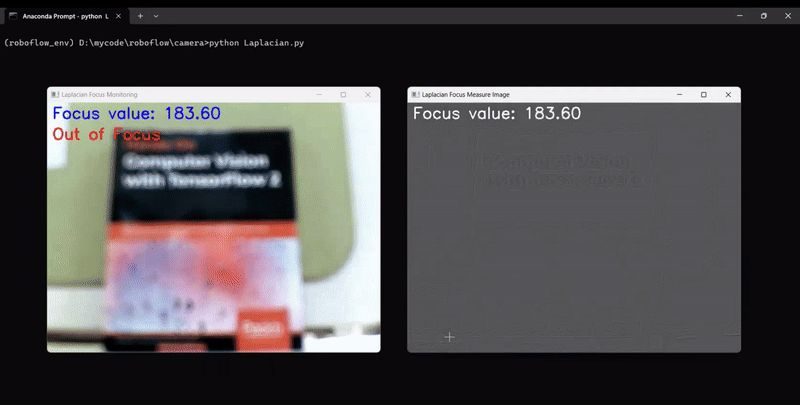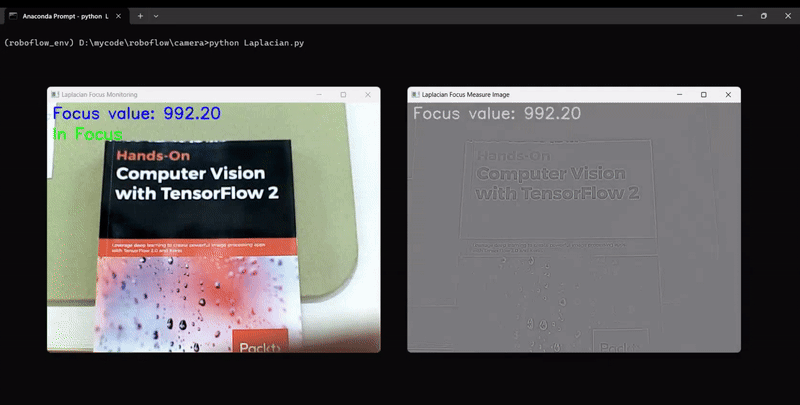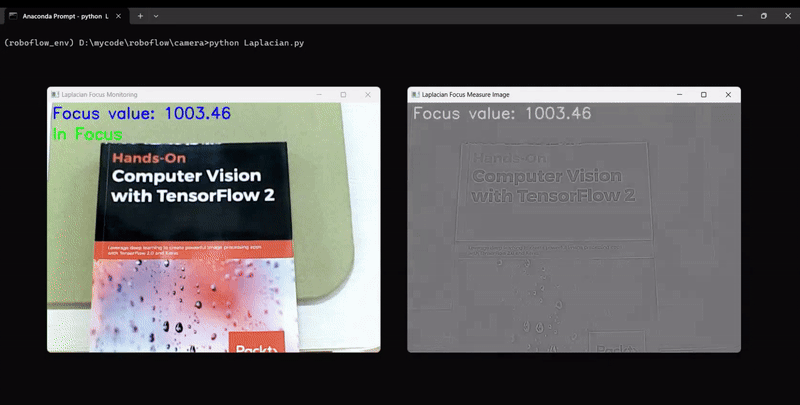
Brenner Function

The Brenner function is used to measure the sharpness of an image by focusing on its intensity changes. This function was introduced in 1971 by Brenner et al. and is widely used in autofocus systems and image quality assessment. The goal of the Brenner function is to assess how "sharp" or "focused" an image is. A sharp image will have more edges and abrupt intensity changes between neighboring pixels. A blurry image, on the other hand, will have smoother transitions and fewer abrupt changes.

Mathematically the Brenner function is defined as:

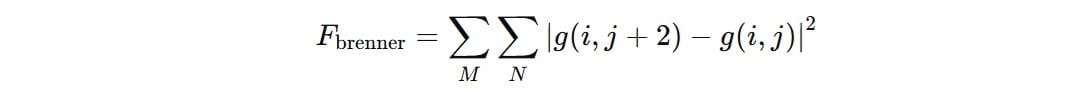
For each pixel in the image, the function compares its intensity with the intensity of the pixel two columns to the right (𝑔(𝑖,𝑗+2)). The difference (𝑔(𝑖,𝑗+2)−𝑔(𝑖,𝑗)) is calculated and is squared to emphasize larger changes and ignore the direction of the change. The squared differences are summed up over all valid pixels.

Now we discuss the steps of the Brenner Algorithm. The code for camera focus using Brenner function, sourced from Roboflow repository, implements a version of the Brenner focus measure. It is used to assess the focus of an image. By definition, the Brenner measure involves computing the sum of squared differences between pixels that are two units apart in the image. However, following code modifies the original definition to enhance it.

Step #1: Convert the Input to Grayscale

First convert the input image to grayscale format since the focus measure works on intensity values. It simplifies calculations as a grayscale image has only one channel.

if len(input_image.shape) == 3:
    input_image = cv2.cvtColor(input_image, cv2.COLOR_BGR2GRAY)

Step #2: Convert to 16-Bit Integer Format

Now we convert the grayscale image to 16-bit signed integers. Because subtracting pixel values gives negative differences therefore it needs to be handled. Using np.int16 allows for negative values without overflow.

converted_image = input_image.astype(np.int16)

Step #3: Initialize Difference Matrices

Next, empty matrices of the same size as the input image to store horizontal and vertical differences are created. These matrices will store the intensity differences between pixels spaced two positions apart.

height, width = converted_image.shape
horizontal_diff = np.zeros((height, width))
vertical_diff = np.zeros((height, width))

Step #4: Calculate Horizontal and Vertical Differences

The horizontal and vertical differences are calculated. The horizontal differences calculate the intensity difference between each pixel and the pixel two columns to the right and the result is stored in the horizontal_diff matrix. The vertical differences calculates the intensity difference between each pixel and the pixel two rows below and the result is stored in the vertical_diff matrix. While canculating the horizontal and vertical differences, negative differences are set to zero using np.clip().

horizontal_diff[:, : width - 2] = np.clip(
    converted_image[:, 2:] - converted_image[:, :-2], 0, None
)
vertical_diff[: height - 2, :] = np.clip(
    converted_image[2:, :] - converted_image[:-2, :], 0, None
)

Step #5: Combine Horizontal and Vertical Differences

The focus measure is then calculated by taking the squared maximum of horizontal and vertical gradients at each pixel, emphasizing sharper regions in the image. focus_measure is a matrix representing the sharpness (focus) measure for each pixel.

focus_measure = np.max((horizontal_diff, vertical_diff), axis=0) ** 2

Step #6: Normalize and convert to 8-Bit for Visualization

In this step the focus measure matrix is normalized to a range of [0,255] and converted into an 8-bit grayscale image for visualization.

focus_measure_image = ((focus_measure / focus_measure.max()) * 255).astype(np.uint8)

Step #8: Return the Outputs

Finally, a normalized visualization of the focus measure is returned as focus_measure_image and a scalar value representing the overall sharpness of the image is returned as focus_measure.mean().

return focus_measure_image, focus_measure.mean()

Overall, the code calculates both horizontal and vertical differences to detect edges in all orientations. As a result, it provides a more robust focus measure compared to traditional Brenner method that consider only horizontal differences. Mean value of all the elements in the focus_measure matrix is calculated which normalizes the focus measure by the number of pixels. This ensures consistency across images of different sizes.

Following is the code for camera focus using Brenner function.

import cv2
import numpy as np
from typing import Tuple

def calculate_brenner_measure(
    input_image: np.ndarray,
    text_color: Tuple[int, int, int] = (255, 255, 255),
    text_thickness: int = 2,
) -> Tuple[np.ndarray, float]:
    """
    Brenner's focus measure.

    Parameters
    ----------
    input_image : np.ndarray
        The input image in grayscale.
    text_color : Tuple[int, int, int], optional
        The color of the text displaying the Brenner value, in BGR format. Default is white (255, 255, 255).
    text_thickness : int, optional
        The thickness of the text displaying the Brenner value. Default is 2.

    Returns
    -------
    Tuple[np.ndarray, float]
        The Brenner image and the Brenner value.
    """
    # Convert image to grayscale if it has 3 channels
    if len(input_image.shape) == 3:
        input_image = cv2.cvtColor(input_image, cv2.COLOR_BGR2GRAY)

    # Convert image to 16-bit integer format
    converted_image = input_image.astype(np.int16)

    # Get the dimensions of the image
    height, width = converted_image.shape

    # Initialize two matrices for horizontal and vertical focus measures
    horizontal_diff = np.zeros((height, width))
    vertical_diff = np.zeros((height, width))

    # Calculate horizontal and vertical focus measures
    horizontal_diff[:, : width - 2] = np.clip(
        converted_image[:, 2:] - converted_image[:, :-2], 0, None
    )
    vertical_diff[: height - 2, :] = np.clip(
        converted_image[2:, :] - converted_image[:-2, :], 0, None
    )

    # Calculate final focus measure
    focus_measure = np.max((horizontal_diff, vertical_diff), axis=0) ** 2

    # Convert focus measure matrix to 8-bit for visualization
    focus_measure_image = ((focus_measure / focus_measure.max()) * 255).astype(np.uint8)

    # Display the Brenner value on the top left of the image
    cv2.putText(
        focus_measure_image,
        f"Focus value: {focus_measure.mean():.2f}",
        (10, 30),
        cv2.FONT_HERSHEY_SIMPLEX,
        1,
        text_color,
        text_thickness,
    )

    return focus_measure_image, focus_measure.mean()

def monitor_focus_brenner():

    cap = cv2.VideoCapture(0)
    if not cap.isOpened():
        print("Error: Camera not accessible.")
        return
    
    # Set a threshold for focus measure (this may need tuning)
    focus_threshold = 500  # Adjust this threshold based on your application

    while True:
        ret, frame = cap.read()
        if not ret:
            break

        focus_measure_image, focus_score = calculate_brenner_measure(frame)
        
        status = "In Focus" if focus_score > focus_threshold else "Out of Focus"
        color = (0, 255, 0) if status == "In Focus" else (0, 0, 255)

        cv2.putText(frame, f"Focus value: {focus_score:.2f}", (10, 30),
                    cv2.FONT_HERSHEY_SIMPLEX, 1, (255, 0, 0), 2)
        cv2.putText(frame, status, (10, 70), cv2.FONT_HERSHEY_SIMPLEX, 1, color, 2)

        cv2.imshow("Brenner Focus Monitoring", frame)
        cv2.imshow("Brenner Focus Measure Image", focus_measure_image)

        if cv2.waitKey(1) & 0xFF == ord('q'):
            break

    cap.release()
    cv2.destroyAllWindows()

if __name__ == "__main__":
    monitor_focus_brenner()

The code will generate output similar to following, showing the camera focus measurement changing as we adjust the camera focus:

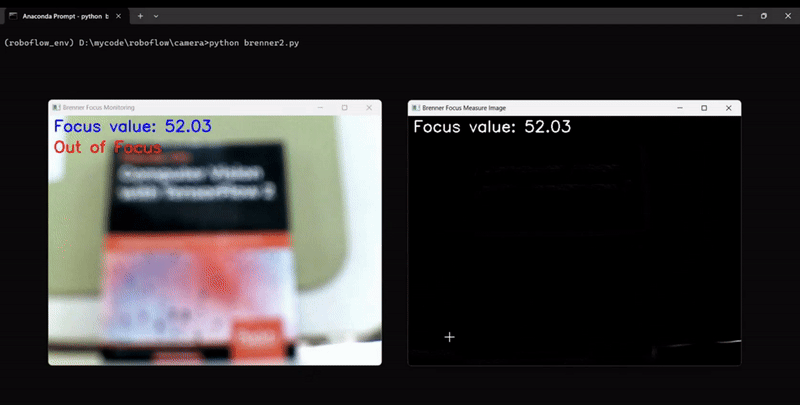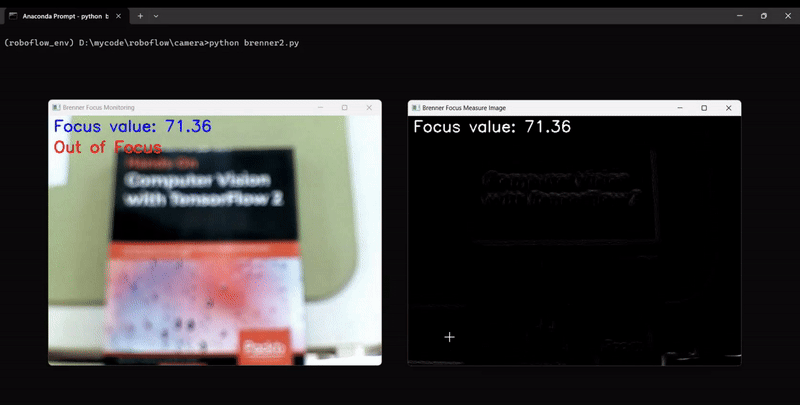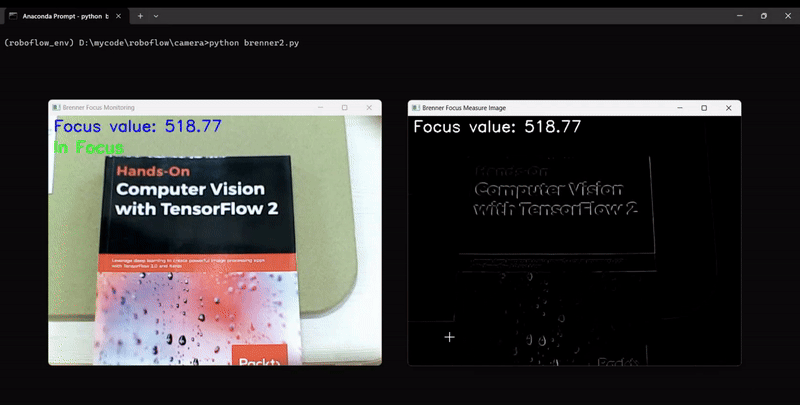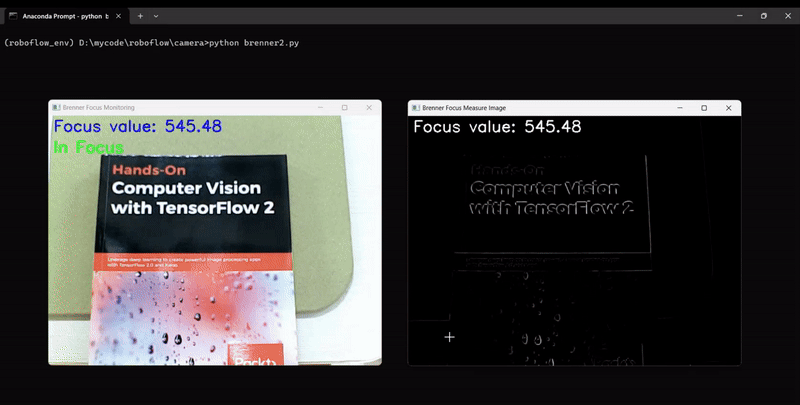
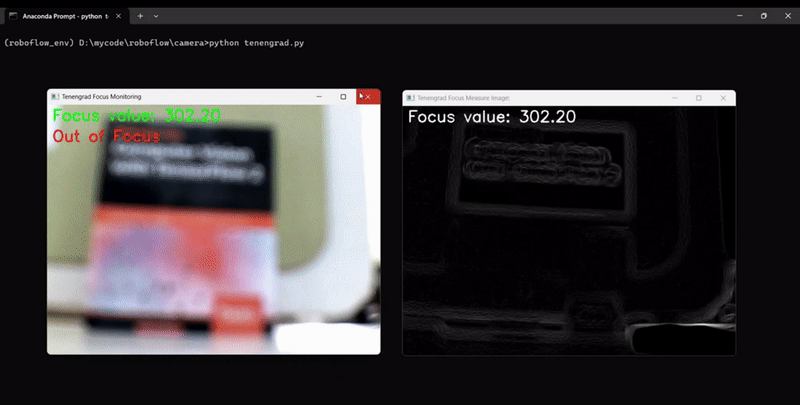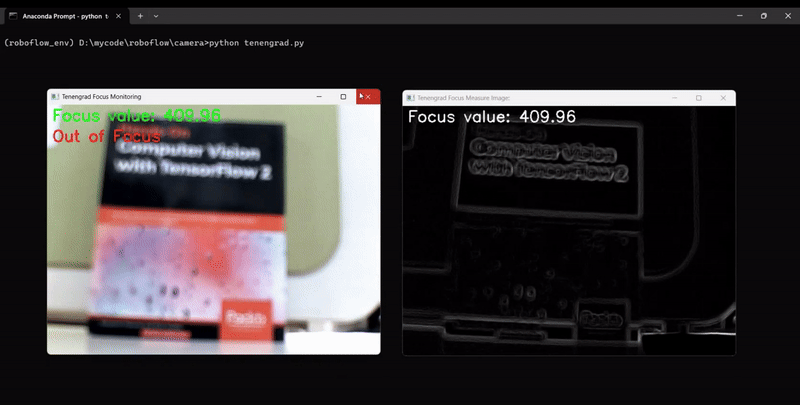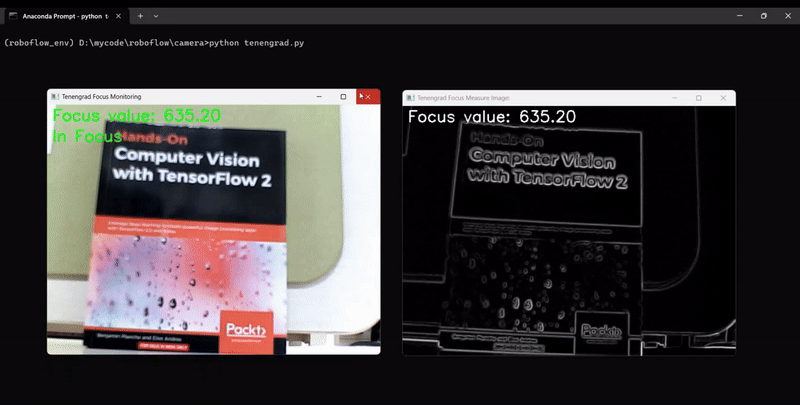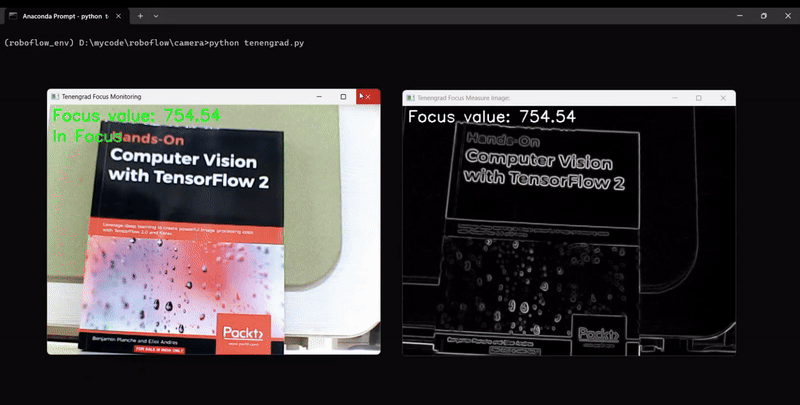
Tenengrad Function

The Tenengrad function is another method used to measure the sharpness or focus of an image by analyzing the gradient strength at each pixel. It evaluates the presence and intensity of edges in the image, which are indicative of sharp transitions in pixel intensity. The function is widely applied in image quality assessment, blur detection, and autofocus systems. This method computes the gradients (𝐺𝑥,𝐺𝑦) of the image, which measure changes in intensity in the horizontal and vertical directions, respectively. The Sobel operator is commonly used to compute these gradients. The sharpness at each pixel is represented by the squared gradient magnitude:

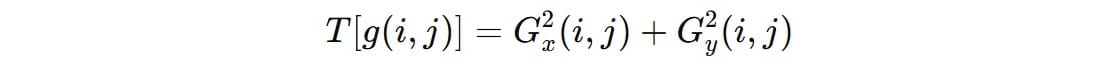
Strong gradient magnitudes indicate sharper edges, while weaker magnitudes suggest blur. The total sharpness of the image is calculated by summing up (or averaging) the gradient magnitudes across all pixels:

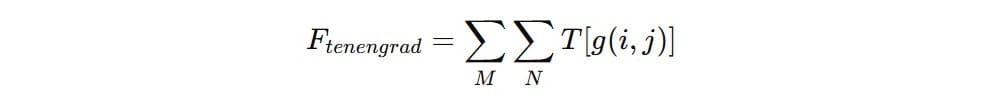
This provides a single scalar value that reflects the overall sharpness of the image. The Tenengrad function is particularly useful in:

• autofocus systems to automatically determine whether an image is in focus.
• blur detection to identify images with motion blur or defocused areas.
• image quality assessment to provide an objective measure of sharpness in imaging systems such as cameras, microscopes, and telescopes.

Steps of the Tenengrad Algorithm in the Code:

Step#1: Convert to Grayscale

The algorithm works on a single channel, so the input image is converted to grayscale:

gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

Step#2 Compute Sobel Gradients

Gradients in the X and Y directions are computed using the Sobel operator.

sx = cv2.Sobel(gray, cv2.CV_32F, 1, 0, ksize=5)
sy = cv2.Sobel(gray, cv2.CV_32F, 0, 1, ksize=5)

Step#3: Calculate Gradient Magnitude

Then, the X and Y gradients are combined to compute the overall gradient magnitude.

magnitude = cv2.magnitude(sx, sy)

Step#4: Compute the Mean Gradient Magnitude

Finally, the mean of the gradient magnitudes is calculated to obtain the focus measure.

return magnitude.mean()

Following is the code for camera focus using Tenengrad function.

import cv2
import numpy as np

def calculate_tenengrad_measure(img):
    """
    Compute the Tenengrad focus measure for an image.
    :param img: Grayscale input image.
    :return: Tuple of mean gradient magnitude and normalized gradient magnitude image.
    """
    # Sobel gradient computation in x and y directions
    sx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=5)
    sy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=5)

    # Compute gradient magnitude
    magnitude = cv2.magnitude(sx, sy)

    # Normalize the gradient magnitude for visualization
    magnitude_normalized = cv2.normalize(magnitude, None, 0, 255, cv2.NORM_MINMAX)

    # Return the mean of the gradient magnitudes and the normalized image
    return magnitude.mean(), magnitude_normalized

def main():
    # Initialize video capture (1 for external camera, 0 for default)
    cap = cv2.VideoCapture(0)

    # Check if the camera opened successfully
    if not cap.isOpened():
        print("Cannot open camera")
        return

    # Set a threshold for focus measure (this may need tuning)
    focus_threshold = 500.0  # Adjust this threshold based on your application

    while True:
        # Capture frame-by-frame
        ret, frame = cap.read()

        # If frame is read correctly ret is True
        if not ret:
            print("Can't receive frame (stream end?). Exiting ...")
            break

        # Convert to grayscale
        gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

        # Compute the focus measure and gradient magnitude visualization
        focus_measure, magnitude_normalized = calculate_tenengrad_measure(gray)

        # Convert normalized gradient magnitude to 8-bit for display
        magnitude_normalized_uint8 = magnitude_normalized.astype(np.uint8)

        # Overlay focus measure score on the normalized gradient magnitude image
        cv2.putText(
            magnitude_normalized_uint8,
            f'Focus value: {focus_measure:.2f}', 
            (10, 30), 
            cv2.FONT_HERSHEY_SIMPLEX, 
            1, 
            (255,),  # White color in grayscale
            2
        )

        # Display the normalized gradient magnitude image with focus measure score
        cv2.imshow('Tenengrad Focus Measure Image:', magnitude_normalized_uint8)

        # Display the original frame with focus measure text
        cv2.putText(frame, f'Focus value: {focus_measure:.2f}', (10, 30),
                    cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 255, 0), 2)

        # Focus alert based on the threshold
        if focus_measure < focus_threshold:
            cv2.putText(frame, 'Out of Focus', (10, 70),
                        cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 0, 255), 2)
        else:
            cv2.putText(frame, 'In Focus', (10, 70),
                        cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 255, 0), 2)

        # Display the resulting frame with focus alert
        cv2.imshow('Tenengrad Focus Monitoring', frame)

        # Exit on pressing 'q'
        if cv2.waitKey(1) & 0xFF == ord('q'):
            break

    # When everything done, release the capture
    cap.release()
    cv2.destroyAllWindows()

if __name__ == "__main__":
    main()

The code will generate output similar to following, showing the camera focus measurement changing as we adjust the camera focus:

Conclusion

Camera focus monitoring is a foundational requirement for deploying robust computer vision systems. By integrating focus monitoring into any computer vision systems, a consistent image quality can be assured to prevent detection errors by computer vision models. In computer vision applications like defect detection system, where precision is paramount, an automated focus monitoring system ensures the system operates at peak accuracy, safeguarding product quality and reducing overall costs. Roboflow offers building no-code camera focus system that you may integrate in your computer vision system. I recommend checking out the post How to Monitor Camera Focus with Computer Vision to learn how to build it.

Cite this Post

Use the following entry to cite this post in your research:

Timothy Malche. (Nov 26, 2024). Camera Focus in Computer Vision: A Guide. Roboflow Blog: https://blog.roboflow.com/computer-vision-camera-focus-guide/

Discuss this Post

If you have any questions about this blog post, start a discussion on the Roboflow Forum.