How to Code Non-Maximum Suppression (NMS) in Plain NumPy

Double Detection in Computer Vision

If you’ve been working with object detection long enough, you’ve undoubtedly encountered the problem of double detection. For some reason, the model detects the same object multiple times on the same image. This is particularly inconvenient if you want to build more advanced analytics — like  counting or tracking detections.

This exact issue occurred during a recent project, and it was quickly solved thanks to Non-Maximum Suppression (NMS). This post will explain how NMS  works and shows you how to code NMS in NumPy.

Ready to Use Non-Maximum Suppression Code

If you are looking for a quick solution to your problem and don’t have time to dive deep into the math and code, there is a pip package to handle it for you. The supervision pip package offers an NMS algorithm, which will allow you to easily filter out unwanted detections regardless of the model you are using. In fact, the image pictured above was created using supervision.

import supervision as sv

results = ...
detections = sv.Detections.from_transformers(transformers_results=results)
detections = detections.with_nms(threshold=0.5)

Intersection over Union

NMS looks for groups of bounding boxes that strongly overlap and then decides which boxes to leave and which to remove. The metric that allows us to measure the level of overlap is called Intersection over Union (IoU).

To obtain IoU, we first need to calculate the area of two individual boxes, A and B, as well as their intersection (I). Then we can use these terms to compute the union (U). Finally, we can divide I by U to get the metric.

Vectorized Intersection over Union

The recipe seems pretty simple, but it can be time-consuming when we need to calculate IoU for tens or hundreds of boxes at once. Fortunately, we can speed up this process with matrix operations.

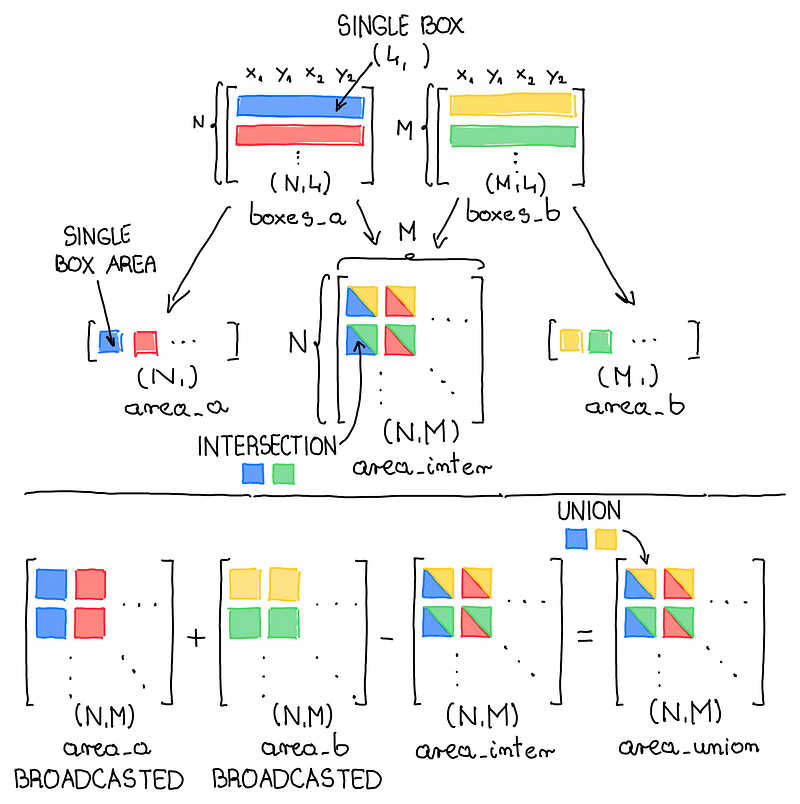
The box_iou_batch function is generic and allows you to calculate the IoU between each box in list A and each box in group B. In our case, these groups are equal to each other and are the set of all detections provided by the model. boxes_a and boxes_b are two-dimensional matrices where each row describes a single box — (x_min, y_min, x_max, y_max).

def box_iou_batch(
	boxes_a: np.ndarray, boxes_b: np.ndarray
) -> np.ndarray:

    def box_area(box):
        return (box[2] - box[0]) * (box[3] - box[1])

    area_a = box_area(boxes_a.T)
    area_b = box_area(boxes_b.T)

    top_left = np.maximum(boxes_a[:, None, :2], boxes_b[:, :2])
    bottom_right = np.minimum(boxes_a[:, None, 2:], boxes_b[:, 2:])

    area_inter = np.prod(
    	np.clip(bottom_right - top_left, a_min=0, a_max=None), 2)
        
    return area_inter / (area_a[:, None] + area_b - area_inter)

Vectorized Non-Maximum Suppression

With an IoU calculating function in place, we are ready to tackle the NMS.

• Start by packing our detections into a 2D matrix. The first 4 columns are occupied by the bounding box coordinates — (x_min, y_min, x_max, y_max), followed by the score and assigned class.
• Sort our matrix decreasingly by score.
• Use box_iou_batch to calculate the IOUs of all bounding boxes with each other.
• Loop over rows of the matrix and, using the information contained in the IoU matrix, discard all detections with the same class and IoU exceeding the defined threshold.

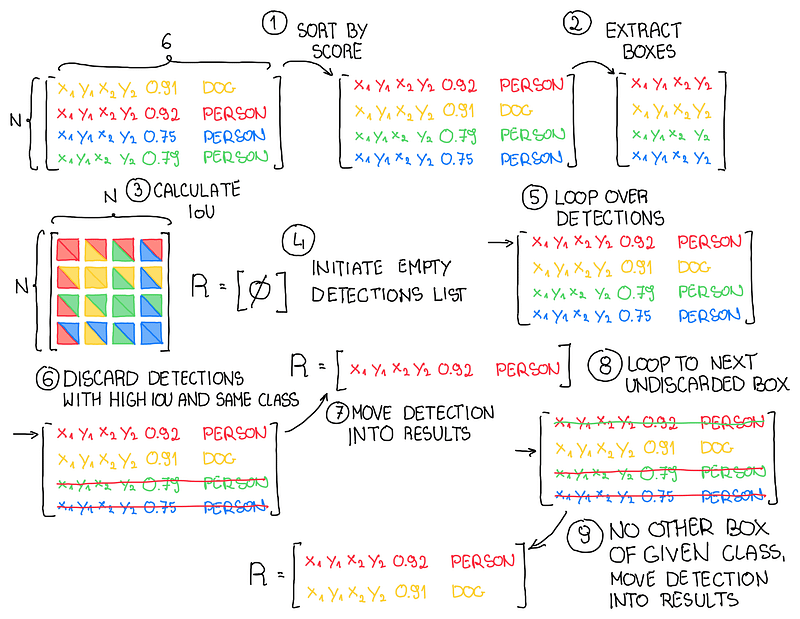
def non_max_suppression(
   predictions: np.ndarray, iou_threshold: float = 0.5
) -> np.ndarray:
    rows, columns = predictions.shape

    sort_index = np.flip(predictions[:, 4].argsort())
    predictions = predictions[sort_index]

    boxes = predictions[:, :4]
    categories = predictions[:, 5]
    ious = box_iou_batch(boxes, boxes)
    ious = ious - np.eye(rows)

    keep = np.ones(rows, dtype=bool)

    for index, (iou, category) in enumerate(zip(ious, categories)):
        if not keep[index]:
            continue

        condition = (iou > iou_threshold) & (categories == category)
        keep = keep & ~condition

    return keep[sort_index.argsort()]

Conclusion

NMS is not magic. It will not solve all your problems with a model. In many cases, however, it can significantly improve the quality of predictions provided by the model and open the way to more advanced object detection analytics. See how to deal with double detections with supervision.

Stay up to date with the projects we are working on at Roboflow and on my GitHub! ⭐

Cite this Post

Use the following entry to cite this post in your research:

Piotr Skalski. (Mar 8, 2023). How to Code Non-Maximum Suppression (NMS) in Plain NumPy. Roboflow Blog: https://blog.roboflow.com/how-to-code-non-maximum-suppression-nms-in-plain-numpy/

Discuss this Post

If you have any questions about this blog post, start a discussion on the Roboflow Forum.