The computer vision community has converged on the metric mAP to compare the performance of object detection systems. In this post, we will dive into the intuition behind how mean Average Precision (mAP) is calculated and why mAP has become the preferred metric for object detection models.
If you prefer to consume this content in video form, we've got you covered. Don't forget to subscribe to our YouTube channel.
What is Object Detection?
Before we consider how to calculate a mean average precision, let's first clearly define the task it is measuring.
Object detection models seek to identify the presence of relevant objects in images and classify those objects into relevant classes. For example, in medical images, we might want to be able to count the number of red blood cells (RBC), white blood cells (WBC), and platelets in the bloodstream. In order to do this automatically, we need to train an object detection model to recognize each one of those objects and classify them correctly. (I did this in a Colab notebook to compare EfficientDet and YOLOv3, two state-of-the-art models for image detection.)
Example Outputs from EfficientDet (green) versus YOLOv3 (yellow)
The models both predict bounding boxes which surround the cells in the picture. They then assign a class to each one of those boxes. For each assignment, the network models a sense of confidence in its prediction. You can see here that we have a total of three classes (RBC, WBC, and Platelets).
How should we decide which model is better? Looking at the image, it looks like EfficientDet (green) has drawn a few too many RBC boxes and missed some cells on the edge of the picture. That is certainly how it feels based on the looks of things - but can we trust an image and intuition? If so, by how much is it better? (Hint: it's not – skip to the bottom if you don't believe.).
It would be nice if we could directly quantify how each model does across images in our test set, across classes, and at different confidence thresholds. Enter mAP!
What is Mean Average Precision (mAP)?
Mean Average Precision (mAP) is used to measure the performance of computer vision models. mAP is equal to the average of the Average Precision metric across all classes in a model. You can use mAP to compare both different models on the same task and different versions of the same model. mAP is measured between 0 and 1.
To understand mean average precision in more detail, we must spend some time discussing confusion matrices, precision, recall, and the precision-recall curve.
What is the Confusion Matrix?
Before we dive deeper, it’s worth taking a moment to explain some of the basic terms we’ll be using in the rest of the blog post. When we evaluate the quality of model detections, we usually compare them with ground truth and divide them into four groups. A case when the model correctly detects an object is called True Positive [TP]. When an object not actually in the image is found, we say it is False Positive [FP].
On the other hand, when an object in the ground truth is not detected, it is False Negative [FN]. The last group is formed by True Negatives [TN]. However, in the case of object detection, it is not taken into account. We can interpret it as all correctly undetected objects — background. The four groups form the so-called confusion matrix, shown in the illustration below.
What is precision and recall?
Precision is a measure of, "when your model guesses how often does it guess correctly?" Recall is a measure of "has your model guessed every time that it should have guessed?" Consider an image that has 10 red blood cells. A model that finds only one of these ten but correctly labels is as "RBC" has perfect precision (as every guess it makes – one – is correct) but imperfect recall (only one of ten RBC cells has been found).
What is the precision-recall curve?
The precision-recall curve, commonly plotted on a graph, shows how recall changes for a given precision and vice versa in a computer vision model. A large area under the curve means that a model has both strong recall and precision, whereas a smaller area under the curve means weaker recall or precision.
Models that involve an element of confidence can tradeoff precision for recall by adjusting the level of confidence they need to make a prediction. In other words, if the model is in a situation where avoiding false positives (stating a RBC is present when the cell was a WBC) is more important than avoiding false negatives, it can set its confidence threshold higher to encourage the model to only produce high precision predictions at the expense of lowering its amount of coverage (recall).
The process of plotting the model's precision and recall as a function of the model's confidence threshold is the precision recall curve. It is downward sloping because as confidence is decreased, more predictions are made (helping recall) and less precise predictions are made (hurting precision).
Think about it like this: if I said, "Name every type of shark," you'd start with obvious ones (high precision), but you'd become less confident with every additional type of shark you could name (approaching full recall with lesser precision). By the way, did you know there are cow sharks?
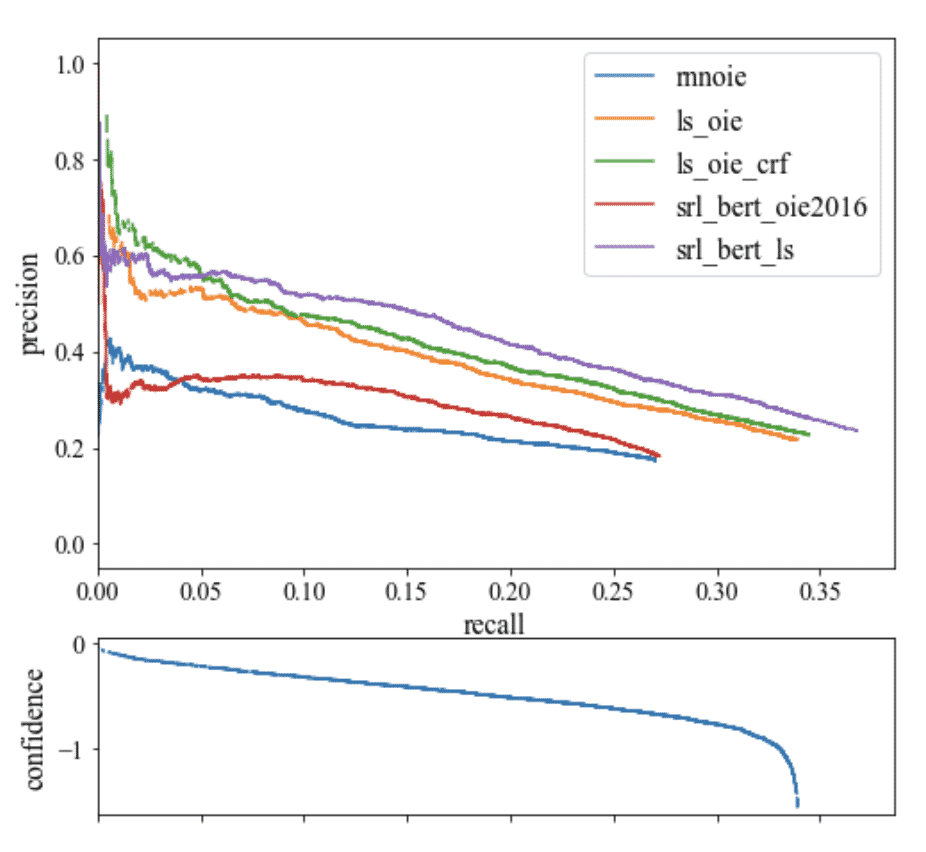
As the model is getting less confident, the curve is sloping downwards. If the model has an upward sloping precision and recall curve, the model likely has problems with its confidence estimation.
AI researchers love metrics and the whole precision-recall curve can be captured in single metrics. The first and most common is F1, which combines precision and recall measures to find the optimal confidence threshold where precision and recall produce the highest F1 value. Next, there is AUC (Area Under the Curve) which integrates the amount of the plot that falls underneath the precision and recall curve.
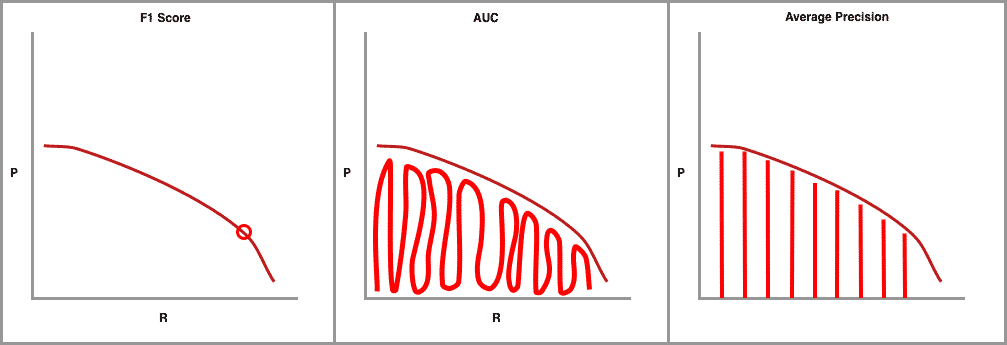
The final precision-recall curve metric is average precision (AP) and of most interest to us here. It is calculated as the weighted mean of precisions achieved at each threshold, with the increase in recall from the previous threshold used as the weight.
Both AUC and AP capture the whole shape of the precision recall curve. To choose one or the other for object detection is a matter of choice and the research community has converged on AP for interpretability.
Measuring Correctness via Intersection over Union
Object detection systems make predictions in terms of a bounding box and a class label.

In practice, the bounding boxes predicted in the X1, X2, Y1, Y2 coordinates are sure to be off (even if slightly) from the ground truth label. We know that we should count a bounding box prediction as incorrect if it is the wrong class, but where should we draw the line on bounding box overlap?
The Intersection over Union (IoU) provides a metric to set this boundary at, measured as the amount of predicted bounding box that overlaps with the ground truth bounding box divided by the total area of both bounding boxes.

Picking the right single threshold for the IoU metric seems arbitrary. One researcher might justify a 60 percent overlap, and another is convinced that 75 percent seems more reasonable. So why not have all of the thresholds considered in a single metric? Enter mAP.
Drawing mAP precision-recall curves
In order to calculate mAP, we draw a series of precision recall curves with the IoU threshold set at varying levels of difficulty.
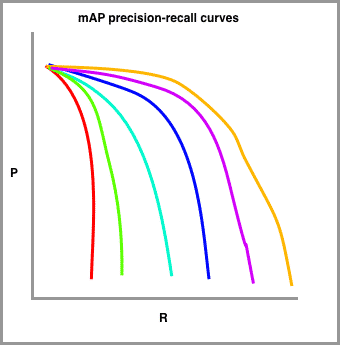
In my sketch, red is drawn with the highest requirement for IoU (perhaps 90 percent) and the orange line is drawn with the most lenient requirement for IoU (perhaps 10 percent). The number of lines to draw is typically set by challenge. The COCO challenge, for example, sets ten different IoU thresholds starting at 0.5 and increasing to 0.95 in steps of .05.
Almost there!
Finally, we draw these precision-recall curves for the dataset split out by class type.
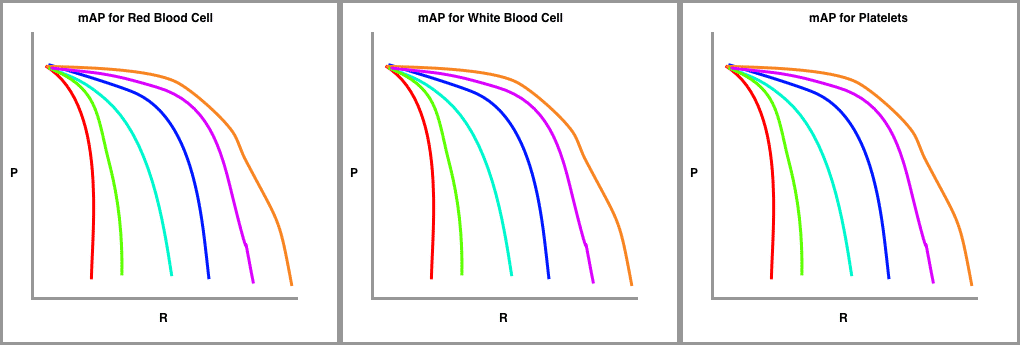
The metric calculates the average precision (AP) for each class individually across all of the IoU thresholds. Then the metric averages the mAP for all classes to arrive at the final estimate. 🤯
The mAP Formula: How to Calculate mAP
The first thing you need to do when calculating the Mean Average Precision (mAP) is to select the IoU threshold. We can choose a single value, for example, 0.5 (mAP@0.5), or a range, for example, from 0.5 to 0.95 with 0.05 increments (mAP@0.5:0.95). In the latter case, we calculate the mAP for each range value and average them.
Increasing the IoU threshold results in more restricted requirements — detections with lower IoU values will be considered false — and thus, the mAP value will drop.
The image above shows the process of calculating an example AP value. First, we take a detection group and draw its PR curve. We do this by iteratively decreasing the confidence threshold from 1.0 to 0.0, calculating Precision [P] and Recall [R] for a given threshold value, and plotting the points on a graph.
AP is equal to the area of the green figure under the graph. It is calculated as the weighted mean of precisions achieved at each threshold, with the increase in recall from the previous threshold used as the weight.
The second thing we need to do is divide our detections into groups based on the detected class. We then compute the Average Precision (AP) for each group and calculate its mean, resulting in an mAP for a given IoU threshold.
You can calculate mAP in Python using the supervision Python package.
To get started, first install supervision:
pip install supervisionYou can calculate mAP with the MeanAveragePrecision class. To use this class, you need:
- A dataset with your ground truth annotations, and;
- A model on which to run inference.
Let's walk through an example of using the class with a YOLOv8 model.
Here is the code you need:
import supervision as sv
from ultralytics import YOLO
dataset = sv.DetectionDataset.from_yolo(...)
model = YOLO(...)
def callback(image: np.ndarray) -> sv.Detections:
result = model(image)[0]
return sv.Detections.from_ultralytics(result)
mean_average_precision = sv.MeanAveragePrecision.benchmark(
dataset = dataset,
callback = callback
)
print(mean_average_precision.map50_95)
# 0.433Above, we initialize an object detection model, load a dataset from the YOLO format with the supervision.DetectionDataset API, then declare a callback function that takes in an image and returns supervision.Detections.
We then pass in our dataset and callback into the MeanAveragePrecision class to calculate mAP. Then, we print the results of mAP50 @ 95 to the console.
You can use this code with a variety of object detection models. To see a full list of models you can use with supervision, refer to the supervision Detections documentation.
Using Mean Average Precision (mAP) in Practice
I recently used mAP in a post comparing state of the art detection models, EfficientDet and YOLOv3. I wanted to see which model did better on the tasks of identifying cells in the bloodstream and identifying chess pieces.
After I had run inference over each image in my test set, I imported a python package to calculate mAP in my Colab notebook. And here were the results!
Evaluation of EfficientDet on cell object detection:
78.59% = Platelets AP
77.87% = RBC AP
96.47% = WBC AP
mAP = 84.31%
Evaluation of YOLOv3 on cell object detection:
72.15% = Platelets AP
74.41% = RBC AP
95.54% = WBC AP
mAP = 80.70%
Contrary to the single inference picture at the beginning of this post, it turns out that EfficientDet did a better job of modeling cell object detection! You will also notice that the metric is broken out by object class. This tells us that WBC are much easier to detect than Platelets and RBC, which makes sense since they are much larger and distinct than the other cells.
mAP is also often broken out into small, medium, and large objects which helps identify where models (and/or datasets) may be going awry.
Conclusion
Now you know how to calculate mAP and more importantly, what it means!
To improve your model’s mAP, take a look at getting started with some data augmentation techniques.
Thanks for reading and may your mean average precisions reach ever skyward 🚀
Frequently Asked Questions
What is mAP used for?
mAP is used to compare the performance of computer vision models. mAP gives computer vision developers a single primary metric on which to compare that encompasses both the precision and recall of a model. Later comparisons may be made on other metrics to better evaluate a model.
What does a high mAP mean?
A high mAP means that a model has both a low false negative and a low false positive rate. The higher the mAP, the more precise and the higher the recall is for your model. Computer vision engineers aim to improve mAP as they build models.