Computer vision data augmentation is a powerful way to improve the performance of our computer vision models without needing to collect additional data. We create new versions of our images based on the originals but introduce deliberate imperfections. This helps our model learn what an object generally looks like rather than having it memorize the specific way objects appear in our training data.
Data augmentation works because it increases the semantic coverage of a dataset. Simply put, we introduce additional life-like examples from which our model can learn. In our recent tests on the various image data augmentation techniques, we saw approximately a six-point increase in mean average precision on our example dataset.
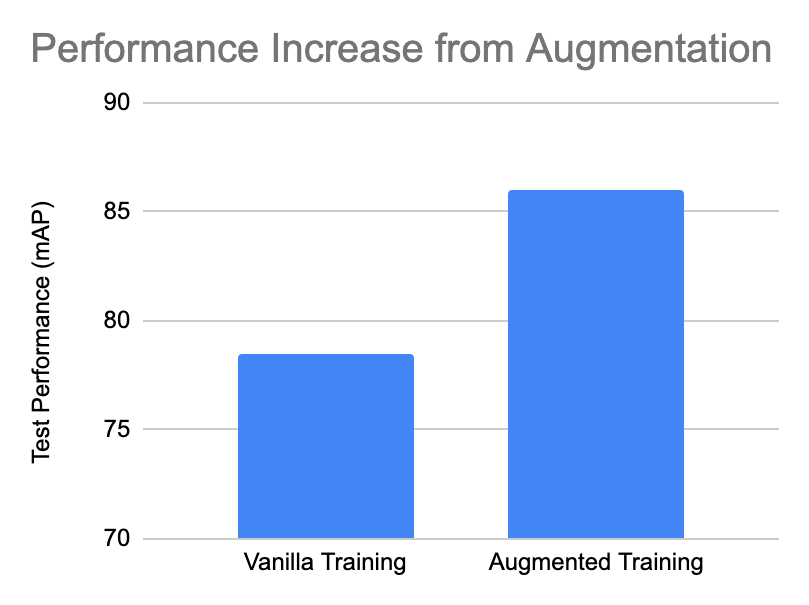
In fact, data augmentation in YOLOv4 is one of the distinguishing reasons the model achieves state-of-the-art performance (a ten-point lift in mAP over prior YOLOv3).
Random Rotation Data Augmentation
One common data augmentation technique is random rotation. A source image is random rotated clockwise or counterclockwise by some number of degrees, changing the position of the object in frame. Notably, for object detection problems, the bounding box must also be updated to encompass the resulting object. (We’ll discuss more about this below.)
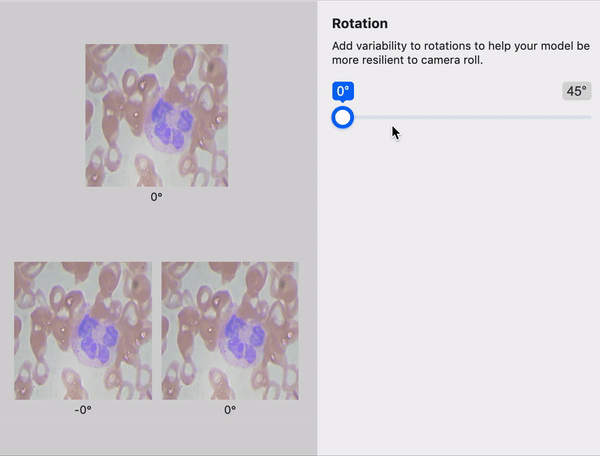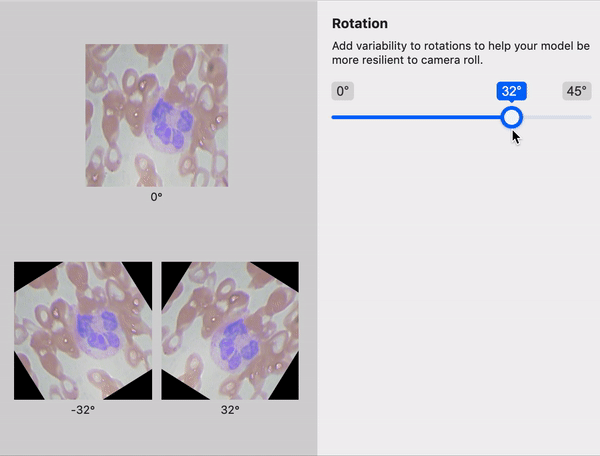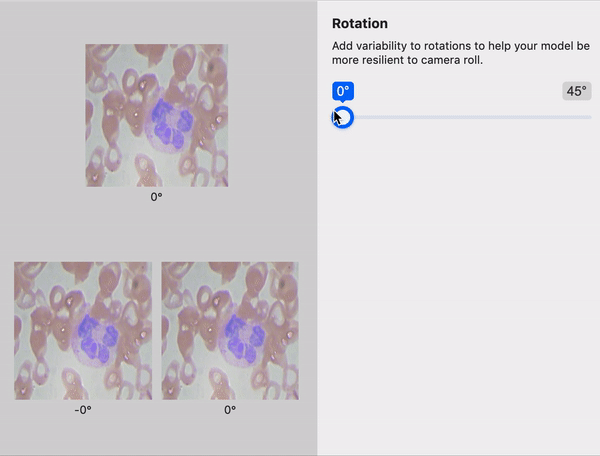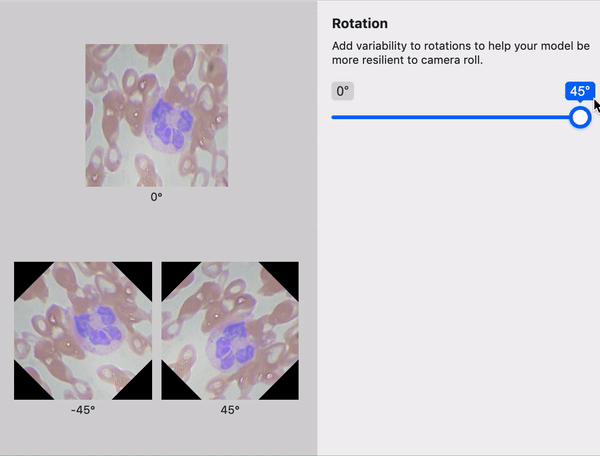
When to Use Random Rotate Augmentation
Random Rotate is a useful augmentation in particular because it changes the angles that objects appear in your dataset during training. Perhaps, during the image collection process, images were only collected with an object horizontally, but in production, the object could be skewed in either direction. Random rotation can improve your model without you having to collect and label more data.
Consider if you were building a mobile app to identify chess pieces. The user may not have their phone perfectly perpendicular to the table where the chess board sets; therefore, chess pieces could appear to be rotated in either direction. In this case, random rotation may be a great choice to simulate what various chess pieces may look like without meticulously capturing every different angle.
Tip: If the camera position is not fixed relative to your subjects (like in a mobile app), random rotation is likely a helpful image augmentation.
Random rotation can also help combat potential overfitting. Even in cases where the camera position is fixed relative to the subjects your model is encountering, random rotation can increase variation to prevent a model from memorizing your training data.
However, like most methods, random rotation is not a silver bullet.
When to Not Use Random Rotate Augmentation
When you perform a data augmentation, it is important to consider everything the augmentation is doing to your images to decide if the augmentation is the right choice for your dataset. In some cases, random rotation may not be the right choice for your dataset.
As a practical note, in order to random rotation an image, note that the image must either have its corners cut off on the top and bottom or have the image increase in size to avoid cropping edges. Note how edges of our chess piece images above are cropped.
Thus, the first reason you should consider not using random rotation is if there is valuable content in the original corners of your images.
Second, after rotation, the image corners are unknown and must be filled with padding. This is the resulting black space we see
Third, you may be a domain setting where objects in the image do not naturally rotate. For example, street signs for a car driving down the road.
Fourth, when the image rotates, the bounding box must as well and the bounding box expands on rotation (unless it is a square). This can be problematic if a lot of your bounding boxes are skinny rectangles because the model will be encouraged to predict much larger objects than it otherwise would. More on this in the implementation.
Ok, you're still convinced!
Let's get cracking on the implementation.
How to Implement Random Rotation in Code (Image)
Now we will dive into the code required to make a random rotation on your image.
All of this code can be executed in this Colab notebook performing random rotation.
To get started, I have put up an example raccoon image for you, and some example annotations.
Note your object annotations may be different, but the flow of this tutorial will still be the same.
Let's take a look at our image and annotations and display our image
!wget https://imgur.com/5MLvXMw.jpg
%mv 5MLvXMw.jpg example.jpg
annotation = {"label":"raccoon","x":150,"y":300,"width":70,"height":200}Displaying our image...
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from PIL import Image
import numpy as np
im = np.array(Image.open('example.jpg'), dtype=np.uint8)
# Create figure and axes
fig,ax = plt.subplots(1)
# Display the image
ax.imshow(im)
# Create a Rectangle patch
height = annotation["height"]
width = annotation["width"]
x = annotation["x"] - (width/2)
y = annotation["y"] - (height/2)
rect = patches.Rectangle((x,y),width,height,linewidth=5,edgecolor='r',facecolor='none')
# Add the patch to the Axes
ax.add_patch(rect)
plt.show()
Next we define the affine warp function. An affine warp is a transformation of an image that preserves parallel lines.
The affine warp multiplies the two dimensional pixel space by the following matrix:
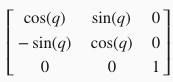
Thankfully the openCV package takes care of most of these details for us and we only define the following:
import numpy as np
import cv2
import math
import copy
def warpAffine(src, M, dsize, from_bounding_box_only=False):
"""
Applies cv2 warpAffine, marking transparency if bounding box only
The last of the 4 channels is merely a marker. It does not specify opacity in the usual way.
"""
return cv2.warpAffine(src, M, dsize)Then we define a function to rotate an image counterclockwise by one angle. First, we get the rotation matrix for a 2D image from cv2. Then, we get the new bounding dimensions of the image from the sine and the cosine of the rotation matrix (above), to adjust the new height and width of the image.
Then we adjust the matrix to keep in mind this height and width translation. And finally perform the affine transformation.
For this example, we rotate by 40 degrees.
def rotate_image(image, angle):
"""Rotate the image counterclockwise.
Rotate the image such that the rotated image is enclosed inside the
tightest rectangle. The area not occupied by the pixels of the original
image is colored black.
Parameters
----------
image : numpy.ndarray
numpy image
angle : float
angle by which the image is to be rotated. Positive angle is
counterclockwise.
Returns
-------
numpy.ndarray
Rotated Image
"""
# get dims, find center
(h, w) = image.shape[:2]
(cX, cY) = (w // 2, h // 2)
# grab the rotation matrix (applying the negative of the
# angle to rotate clockwise), then grab the sine and cosine
# (i.e., the rotation components of the matrix)
M = cv2.getRotationMatrix2D((cX, cY), angle, 1.0)
cos = np.abs(M[0, 0])
sin = np.abs(M[0, 1])
# compute the new bounding dimensions of the image
nW = int((h * sin) + (w * cos))
nH = int((h * cos) + (w * sin))
# adjust the rotation matrix to take into account translation
M[0, 2] += (nW / 2) - cX
M[1, 2] += (nH / 2) - cY
# perform the actual rotation and return the image
image = warpAffine(image, M, (nW, nH), False)
# image = cv2.resize(image, (w,h))
return imageLet's take a look!
from skimage.io import imread
img_path = 'example.jpg'
im = imread(img_path).astype(np.float64) / 255
from skimage import data, io
from matplotlib import pyplot as plt
rotated = crop_to_center(im, rotate_image(im, 40))
io.imshow(rotated)
plt.show()
Now, the problem here is that the transformation has changed the dimensions of our image. In order to correct for this, we implement a crop to center to return to the original image's dimensions.
def crop_to_center(old_img, new_img):
"""
Crops `new_img` to `old_img` dimensions
:param old_img: <numpy.ndarray> or <tuple> dimensions
:param new_img: <numpy.ndarray>
:return: <numpy.ndarray> new image cropped to old image dimensions
"""
if isinstance(old_img, tuple):
original_shape = old_img
else:
original_shape = old_img.shape
original_width = original_shape[1]
original_height = original_shape[0]
original_center_x = original_shape[1] / 2
original_center_y = original_shape[0] / 2
new_width = new_img.shape[1]
new_height = new_img.shape[0]
new_center_x = new_img.shape[1] / 2
new_center_y = new_img.shape[0] / 2
new_left_x = int(max(new_center_x - original_width / 2, 0))
new_right_x = int(min(new_center_x + original_width / 2, new_width))
new_top_y = int(max(new_center_y - original_height / 2, 0))
new_bottom_y = int(min(new_center_y + original_height / 2, new_height))
# create new img canvas
canvas = np.zeros(original_shape)
left_x = int(max(original_center_x - new_width / 2, 0))
right_x = int(min(original_center_x + new_width / 2, original_width))
top_y = int(max(original_center_y - new_height / 2, 0))
bottom_y = int(min(original_center_y + new_height / 2, original_height))
canvas[top_y:bottom_y, left_x:right_x] = new_img[new_top_y:new_bottom_y, new_left_x:new_right_x]
return canvas
Image complete! If you are doing classification, you may stop here. For object detection, we need to continue onward to rotate the bounding box.
How to Implement Random Rotation in Code (Bounding Box)
To rotate the bounding box, we need to take the original bounding box and translate it about the origin for the same rotation angle that the image was rotated. Then, our bounding box will be somewhat diamond shaped and we will need to draw a larger bounding box (blue) around it to make sure that we capture our target.
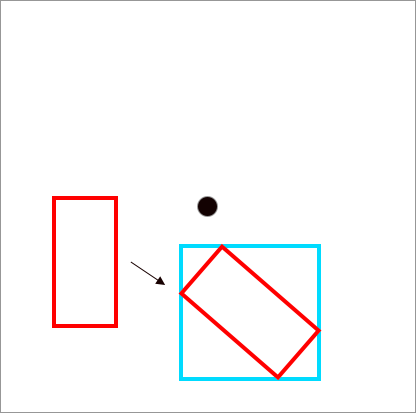
To implement this, we first define a function to rotate a point about the origin like so:
def rotate_point(origin, point, angle):
"""
Rotate a point counterclockwise by a given angle around a given origin.
:param angle: <float> Angle in radians.
Positive angle is counterclockwise.
"""
ox, oy = origin
px, py = point
qx = ox + math.cos(angle) * (px - ox) - math.sin(angle) * (py - oy)
qy = oy + math.sin(angle) * (px - ox) + math.cos(angle) * (py - oy)
return qx, qyThen we define our annotation rotation function with the following steps. First we rotate the middle of the image about the origin, then we rotate each point about the origin. Then, we calculate the maximum distance between points for the width and height dimensions of the final bounding box.
def rotate_point(origin, point, angle):
"""
Rotate a point counterclockwise by a given angle around a given origin.
:param angle: <float> Angle in radians.
Positive angle is counterclockwise.
"""
ox, oy = origin
px, py = point
qx = ox + math.cos(angle) * (px - ox) - math.sin(angle) * (py - oy)
qy = oy + math.sin(angle) * (px - ox) + math.cos(angle) * (py - oy)
return qx, qy
def rotate_annotation(origin, annotation, degree):
"""
Rotates an annotation's bounding box by `degree`
counterclockwise about `origin`.
Assumes cropping from center to preserve image dimensions.
:param origin: <tuple> down is positive
:param annotation: <dict>
:param degree: <int> degrees by which to rotate
(positive is counterclockwise)
:return: <dict> annotation after rotation
"""
# Don't mutate annotation
new_annotation = copy.deepcopy(annotation)
# new_annotation = annotation
angle = math.radians(degree)
origin_x, origin_y = origin
origin_y *= -1
x = annotation["x"]
y = annotation["y"]
new_x, new_y = map(lambda x: round(x * 2) / 2, rotate_point(
(origin_x, origin_y), (x, -y), angle)
)
new_annotation["x"] = new_x
new_annotation["y"] = -new_y
width = annotation["width"]
height = annotation["height"]
left_x = x - width / 2
right_x = x + width / 2
top_y = y - height / 2
bottom_y = y + height / 2
c1 = (left_x, top_y)
c2 = (right_x, top_y)
c3 = (right_x, bottom_y)
c4 = (left_x, bottom_y)
c1 = rotate_point(origin, c1, angle)
c2 = rotate_point(origin, c2, angle)
c3 = rotate_point(origin, c3, angle)
c4 = rotate_point(origin, c4, angle)
x_coords, y_coords = zip(c1, c2, c3, c4)
new_annotation["width"] = round(max(x_coords) - min(x_coords))
new_annotation["height"] = round(max(y_coords) - min(y_coords))
return new_annotationAnd finally we try it out on our annotation :
origin = (im.shape[1] / 2, im.shape[0] / 2)
new_annot = rotate_annotation(
origin, annotation, 40
)Visualizing the new bounding box:
from skimage import data, io
from matplotlib import pyplot as plt
rotated = rotate_image(im, 40)
rotated = crop_to_center(im, rotated)
fig,ax = plt.subplots(1)
io.imshow(rotated)
# Create a Rectangle patch
height = new_annot["height"]
width = new_annot["width"]
x = new_annot["x"] - (width/2)
y = new_annot["y"] - (height/2)
rect = patches.Rectangle((x,y),height,width,linewidth=5,edgecolor='b',facecolor='none')
# Add the patch to the Axes
ax.add_patch(rect)
plt.show()
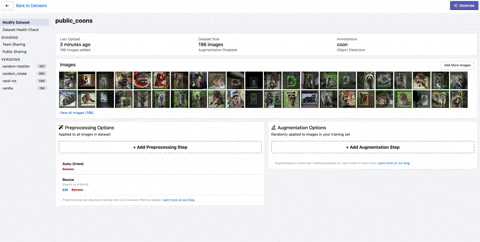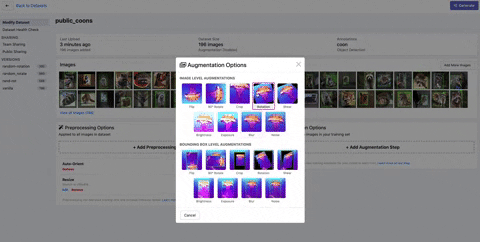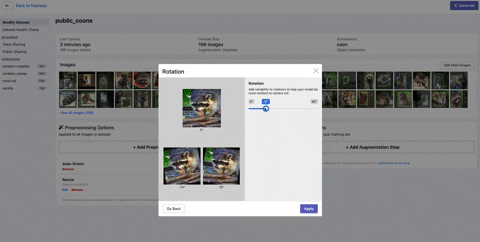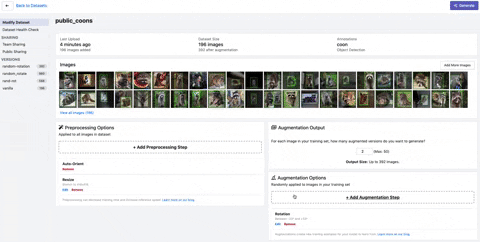
How to Implement Random Rotation in Roboflow
In order to implement random rotation at a dataset level, you need to keep track of multiple annotations across all of your images as you randomly rotate them. This can be quite tricky in practice.
We have implemented a solution to random rotate for the dataset level at Roboflow. Once you have loaded in your dataset with drag and drop functionality in any format, you can perform image augmentations including random rotate by selecting the augmentations you would like to perform and the number of derivative images.
Conclusion
In this tutorial, we have covered how to augment computer vision data with random rotation. We have discussed why to use random rotation and special situations where you might want to avoid it. We covered code together to implement your own images as well as looked at an automated solution through Roboflow.
Thanks for reading! Happy augmenting 🧐
Cite this Post
Use the following entry to cite this post in your research:
Jacob Solawetz. (Jun 24, 2020). Why and How to Implement Random Rotate Data Augmentation. Roboflow Blog: https://blog.roboflow.com/why-and-how-to-implement-random-rotate-data-augmentation/
Discuss this Post
If you have any questions about this blog post, start a discussion on the Roboflow Forum.